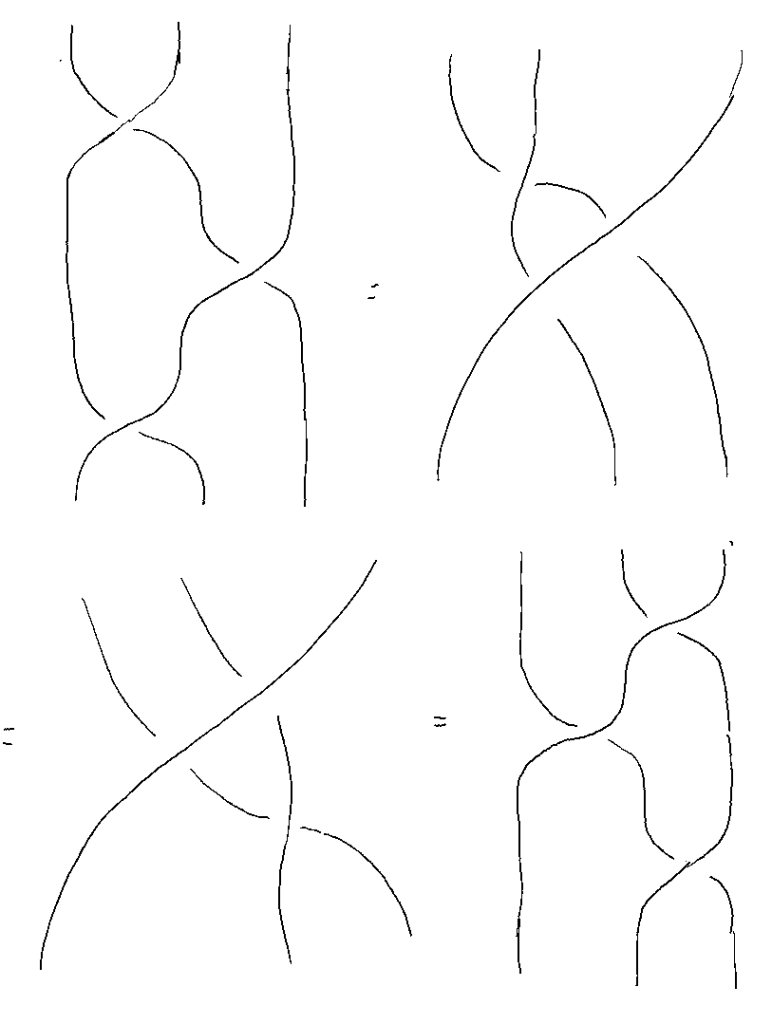
In this second blog post, I introduce monoidal categories which are categories with extra data which allows for their description in terms of diagrams. Equations for a monoidal category are correct if their diagrammatic representation holds up to planar (2D) isotopy. But by introducing braidings, and forming braided monoidal categories, one also has a diagrammatic language which represents equations in braided monoidal categories as diagrams up to spatial (3D) isotopy. I introduce these notions and some related concepts here. Here is the Yang-Baxter equations in diagrammatic form, which holds true in a braided monoidal category: